円の体積の求め方｜は間違い？正しい求め方を中学生でもわかるように解説

2025年10月3日

「円の体積の求め方」で検索すると、円柱や球の公式がたくさん出てきて混乱していませんか。特に中学生がつまずきやすいポイントですよね。

そもそも円（平面）には体積はなく、あるとするならば円柱・円錐・球となります。ここでは円柱・円錐・球のことを指して説明します。実は、これらの公式はバラバラに覚える必要はありません。たった一つの基本を理解すれば、公式を丸暗記しなくても大丈夫です。

この記事では、円柱・円錐・球の体積の求め方を、それぞれの関係性から分かりやすく解説します。「4/3πr^3の覚え方は？」といった疑問も解決し、応用問題まで自信を持って解けるようになりますよ。

✅この記事を読むとわかること

公式を丸暗記せず、立体同士の関係性で体積を理解する方法
円錐や球の体積公式にある分数の「なぜ？」がわかる理由
高さが不明な円錐など、応用問題の具体的な解き方の手順
公式を忘れても、基本から自分で答えを導き出すための思考法

⚠️本記事で使用した注釈のない画像は説明のためのイメージ画像です。実際のデザインとは異なる場合があります。

🔍この記事のまとめ（先に知りたい方へ）

「円の体積」は存在せず、本当に知りたいのは円柱・円錐・球の求め方です。
3つの公式はバラバラではなく、基準となる「円柱」との関係性で全てつながっています。
この記事を読めば、公式を丸暗記せず「なぜ？」から理解でき、応用問題まで解けるようになります。

【円の体積】求め方の公式を”丸暗記”で終わらせない方法

このセクションでは、「円の体積」という疑問から出発し、まずは円柱・円錐・球という3つの立体の関係性を理解します。公式をただ覚えるのではなく、「なぜその形になるのか？」を視覚的に解き明かし、忘れられない知識に変えていきましょう。

まずは結論：「円の体積」ではなく3つの立体を学ぶ

「円の体積の求め方が知りたい」と思って検索したのに、「数学的に円に体積はありません」と言われて、少し混乱してしまったかもしれませんね。たしかに、ノートに描くような平面の「円」には面積しかありません。

でも、ご安心ください。あなたが本当に知りたかったのは、きっと「円」を基にした立体、つまり私たちの身の回りにある「円柱」や「円錐」、「球」の体積のことではないでしょうか。

この記事では、公式をただ紹介して「覚えてください」で終わらせることはしません。なぜその公式になるのか、3つの立体の関係性を解き明かしながら、根本からスッキリ理解することを目指します。そうすれば、公式を忘れてしまっても、自分で思い出せるようになります。

丸暗記から卒業し、本当の意味で「わかる」楽しさを一緒に体験していきましょう。

公式を忘れても大丈夫！全ての基本は「円柱」

数学のテスト前、「公式がたくさんあって覚えられない…」と焦ってしまう気持ち、よくわかります。しかし、これから学ぶ3つの立体のうち、たった一つだけ、基本となる考え方をマスターすれば、驚くほど見通しが良くなります。

その主役こそが「円柱」です。

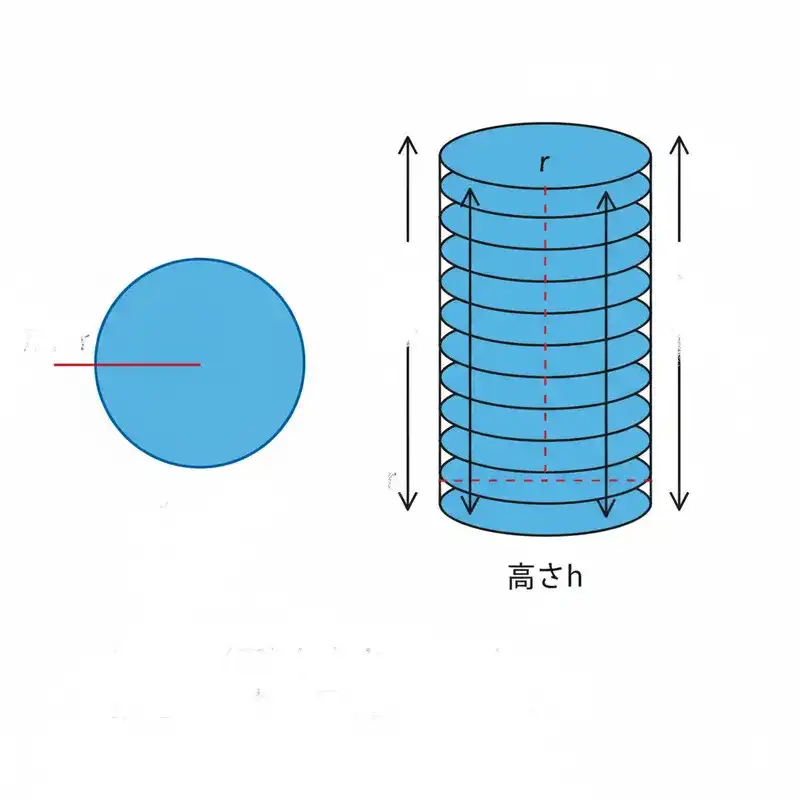
底面積を積み重ねるイメージ

円柱の体積を求める考え方は、とてもシンプルです。

まず、地面に置かれた底面、つまり「円の面積」を求めます。円の面積の公式は「半径 × 半径 × 円周率(π)」でしたね。

次に、その円を一枚のコインだと想像してみてください。そのコインを、円柱の高さの分だけ、まっすぐ上に積み重ねていくのです。この積み重なったコインの束こそが、円柱の体積そのものを表しています。

全ての基本「底面積 × 高さ」

このイメージから、円柱の体積公式が導き出されます。

円柱の体積 (V) = 底面積 (S) × 高さ (h)
V = (π × r²) × h = πr²h

この「底面積を高さの分だけ積み重ねる」という考え方は、三角柱や四角柱など、他の柱体の体積を求めるときも全く同じです。

まずはこの円柱をしっかりと理解することが、丸暗記に頼らないための最初の、そして最も重要な一歩になります。

なぜ円錐の体積は円柱の1/3？理由を図で理解

円錐の体積公式には、V = 1/3πr²h という形で、必ず「1/3」という数字が登場します。「なぜ3分の1なの？」と、不思議に思ったことはありませんか。この数字も、理由を知れば決して謎の存在ではありません。

ここでも活躍するのが、先ほど学んだ「円柱」です。

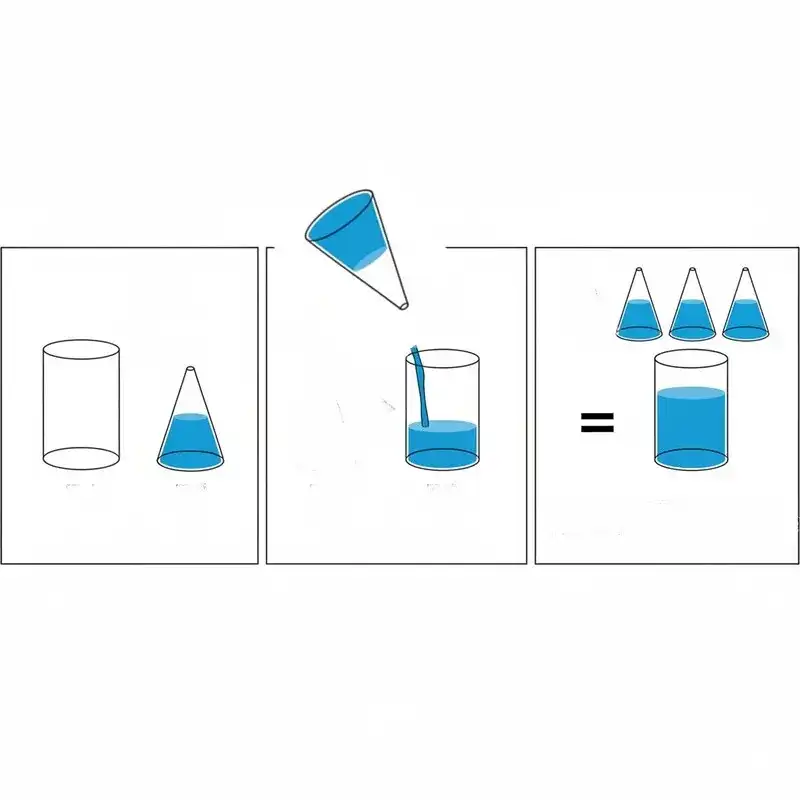
円柱と比べてみよう

ここに、底面の円の大きさと高さが全く同じ「円柱」と「円錐」の形をした容器があると想像してみてください。

もし、円錐の容器いっぱいに水を入れて、それを円柱の容器に注いだら、どのくらいまで溜まるでしょうか。

実は、ちょうど3回繰り返すと、円柱の容器が水でいっぱいになります。

「とんがり帽子は1/3」

この実験が意味することは、とてもシンプルです。

円錐の体積 = 同じサイズの円柱の体積 × 1/3

つまり、円柱の体積 πr²h に 1/3 を掛けるだけで、円錐の体積が求められるのです。

数学の世界では、「～すい」と名前がつく角錐（三角錐や四角錐）も、対応する角柱の体積の1/3になります。

「とんがり帽子のような形（錐体）は、柱体の1/3」と、理由とセットで覚えておけば、公式に迷うことはもうありません。

球の体積は円柱の2/3？アルキメデスの発見

さて、最後は「球」です。V = 4/3πr³ という公式は、分数や3乗が登場し、一見すると円柱や円錐とは全く関係ないように見えるかもしれません。

しかし、この公式にも、円柱との驚くべきつながりが隠されています。これを発見したのは、今から2000年以上も昔の天才数学者、アルキメデスでした。

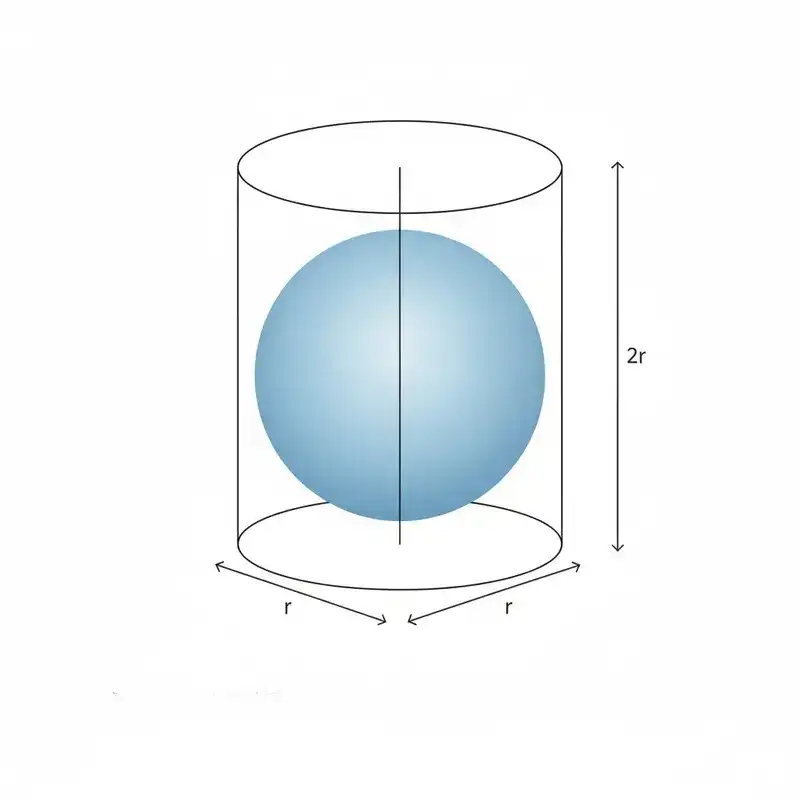
球がピッタリはまる円柱

ある球が、まるで専用ケースのように隙間なくピッタリと収まる円柱を思い浮かべてください。

このとき、円柱の底面の半径は、球の半径「r」と同じになります。そして、円柱の高さは、球の直径である「2r」と等しくなります。

アルキメデスは、この「球の体積」が、外側にピッタリはまる「円柱の体積」の、ちょうど「2/3」になることを発見したのです。

計算で公式を導き出す

本当にそうなるか、計算して確かめてみましょう。

円柱の体積 = 底面積 × 高さ
= (πr²) × (2r) = 2πr³
球の体積 = (2πr³) × 2/3 = 4/3πr³

いかがでしょうか。見事に、私たちが知っている球の体積の公式になりました。複雑に見えた公式も、円柱との関係性を知ることで、その成り立ちから理解することができます。

表面積も公式の関係性で覚えると忘れない

体積の求め方を理解したところで、よく混同しやすい「表面積」の公式も、関係性で覚えるコツをお伝えします。テストで「どっちがどっちだっけ？」と悩む時間をなくしましょう。

「3乗」と「2乗」の違いを意識しよう

公式を覚えるヒントは、単位に隠されています。

体積の単位： cm³（立方センチメートル）
面積の単位： cm²（平方センチメートル）

3乗（³）は体積、2乗（²）は面積を表します。

体積は「3乗」なので、球の体積公式 4/3πr³ では半径が r³ になります。
一方、面積は「2乗」なので、球の表面積公式 S = 4πr² では半径が r² になります。
このように単位とセットで意識すれば、r³とr²を取り違えるミスを防げます。

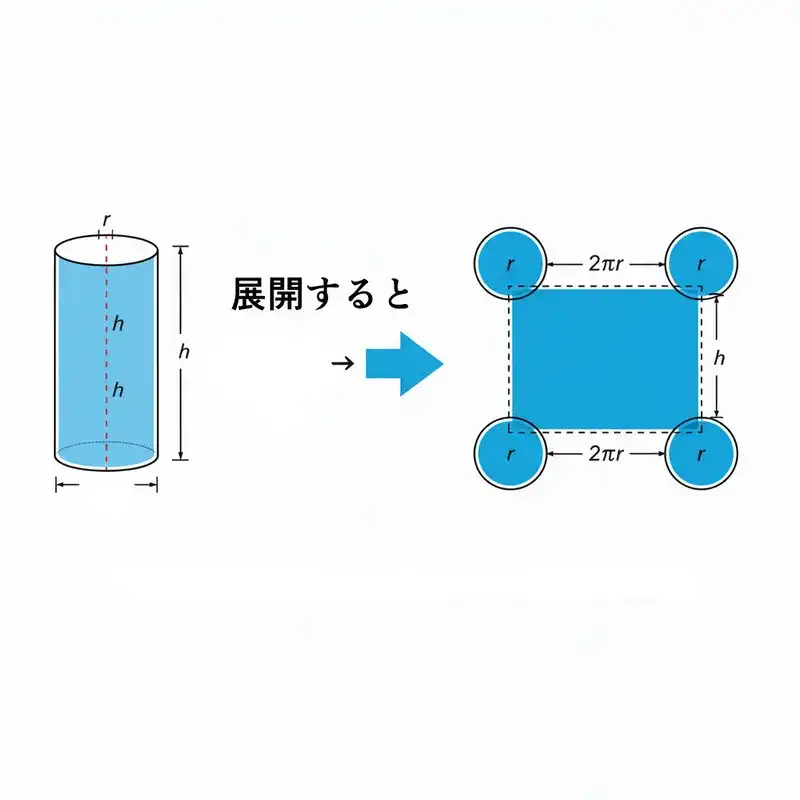
円柱の表面積は「展開図」で考える

円柱の表面積の公式 S = 2πr² + 2πrh を、ただの文字の羅列として覚える必要はありません。円柱をカッターで切り開いて、展開図をイメージしてみてください。

そこには、2つのパーツしかありません。

上下にあるフタの部分です。形は円なので、面積は πr²。それが2つあるので 2πr² となります。
側面を切り開くと、ただの長方形になります。長方形の面積は「縦 × 横」で求められますね。
- 縦 = 円柱の高さ (h)
- 横 = 底面の円周 (2πr)

この2つのパーツの面積を足し合わせるだけ、と考えれば、公式はいつでも自分で作ることができます。

応用問題で試す！本当の「円の体積求め方」

前半で理解した公式の知識が本当に身についたか、さまざまな応用問題で試してみましょう。基本的な計算のコツから、入試で差がつく発展問題まで、解き方の手順と考え方を丁寧に解説します。

【基本】直径や高さが不明なときの対処法

「公式は覚えたはずなのに、なぜか答えが合わない…」そんな経験はありませんか。特に、テスト本番の緊張感の中では、問題文の小さなワナに気づかず、悔しい思いをすることも少なくありません。

ここでは、そんなケアレスミスを防ぎ、基本問題を確実に得点するための2つの対処法と、計算を楽にするテクニックを紹介します。

ワナ①：「直径」が与えられた場合

問題文で「半径」ではなく「直径」が示されるのは、よくある引っかけ問題の一つです。公式に出てくるのは、あくまで「半径（r）」である、という点を常に意識しましょう。

もし、底面の直径が10cm、高さが5cmの円柱の体積を求める問題が出たとします。

間違いやすい計算
π × 10² × 5 = 500π
これは間違いです。
正しい計算
1. まず、直径を2で割って半径を求めます。
  半径 = 10cm ÷ 2 = 5cm
2. 求めた半径を使って体積を計算します。
  V = π × 5² × 5 = 125π cm³

「直径」という言葉を見たら、すぐに「÷2」とメモする癖をつけるだけで、ミスは劇的に減ります。

ワナ②：高さを「逆算」する必要がある場合

時には、体積と底面積が先に与えられて、高さを求めさせる問題もあります。これも、基本の公式に当てはめて、方程式を解くだけです。

体積が225π cm³、底面の半径が5cmの円柱の高さを求めてみましょう。

基本の公式 V = πr²h に、わかっている数字を代入します。
225π = π × 5² × h
計算できる部分を進めます。
225π = 25π × h
両辺を 25π で割って、hを求めます。
h = 225π ÷ 25π = 9cm

慌てず、公式に数値を当てはめれば、答えはおのずと見えてきます。

計算を楽にするちょっとしたコツ

円周率(π)を含む計算では、πの計算を一番最後に行うのが鉄則です。先に3.14などを掛けてしまうと、数字が複雑になり計算ミスのもとになります。πは文字と同じように扱い、最後まで残しておきましょう。

【発展】三平方の定理が必要な円錐の体積問題

問題集の応用問題に進むと、突然「高さ」が書かれていない円錐が登場し、手が止まってしまった経験はないでしょうか。与えられているのは、斜めの線である「母線」の長さと、底面の半径だけ。

これは、一見すると意地悪な問題に見えるかもしれません。しかし、実はこの問題、「あること」に気づけるかどうかを試す、図形問題の面白さが詰まった良問なのです。

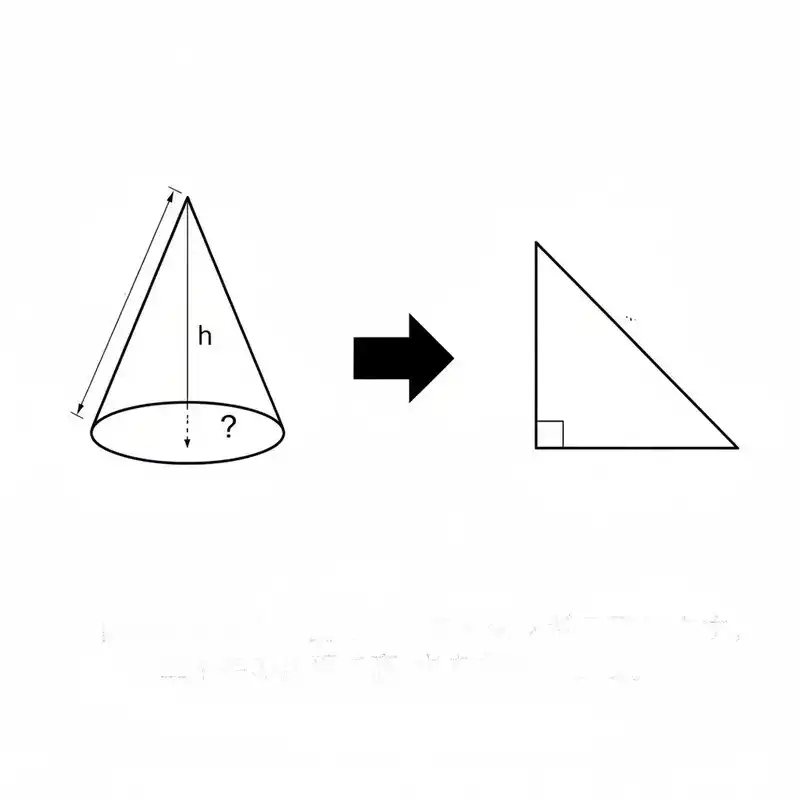
隠れたヒントは「断面図」にあり

攻略のカギは、立体である円錐を、真正面から見た「平面」として捉え直すことにあります。

円錐を真横から見ると、それは「二等辺三角形」に見えますね。そして、その頂点から底面の中心にまっすぐ線を下ろすと、そこには2つの「直角三角形」が現れます。

「三平方の定理」で高さを求める

この直角三角形の3つの辺こそが、問題を解くためのヒントです。

斜辺 → 円錐の「母線」
底辺 → 底面の「半径」
高さ → 円錐の「高さ」

ここまでくれば、もうお分かりですね。中学2年生で学ぶ「三平方の定理（a² + b² = c²）」を使えば、不明だった高さを計算できるのです。

斜辺が10cm、底辺が6cmの直角三角形ができます。求める高さはhです。
h² + 6² = 10²
h² + 36 = 100
h² = 100 – 36 = 64
h = 8 cm （高さなので、マイナスはありえません）
V = 1/3 × π × 6² × 8 = 96π cm³

このように、直接見えないものを、別の知識を使ってあぶり出す。この「ひと手間」こそが、応用問題を解く楽しさであり、入試でライバルと差がつく重要なポイントになります。

【発展】水があふれる？水槽と鉄球の問題に挑戦

「円柱の水槽に入った水に、鉄の球を沈めると、水はどれだけあふれますか？」

これは、複数の立体の体積計算を組み合わせる、応用問題の代表格です。文章が長くて状況が複雑に見えるため、苦手意識を持つ人も多いかもしれません。

しかし、この問題も一つ一つの要素に分解して、順序立てて考えれば、決して難しくはありません。

問題をシンプルに整理する

この問題の核心は、次のシンプルな引き算に気づけるかどうかです。

あふれる水の体積 = 沈める鉄球の体積 – 水槽の空きスペースの体積

鉄球の体積が、水槽の上部の空いているスペースの体積よりも大きければ、その差の分だけ水があふれ出します。

ステップで解いてみよう

底面の半径が4cm、高さが10cmの円柱状の水槽に、高さ8cmまで水が入っています。この水槽に、半径3cmの鉄球を静かに入れます。あふれる水の体積を求めてみましょう。

V(球) = 4/3π × 3³ = 36π cm³
水が入っていない部分の高さは 10cm – 8cm = 2cm です。
この空きスペースも円柱の形をしているので、
V(空き) = (π × 4²) × 2 = 32π cm³
鉄球の体積(36π)は、空きスペースの体積(32π)よりも大きいですね。したがって、水はあふれます。
あふれる水の量 = 36π – 32π = 4π cm³

答えは 4π cm³ となります。

一見すると複雑な問題も、状況を正しく整理し、必要なパーツを一つずつ計算していく。この論理的な思考プロセスこそが、応用力を養う上で最も大切な力となります。

【難問】円錐にボールを入れる問題の考え方

図形問題の中でも、最難関レベルに位置するのが、円錐の中に球がぴったりと収まっているような問題です。

「この球の半径や体積を求めなさい」と言われても、図の中にはヒントとなる長さがほとんど書かれておらず、どこから手をつけていいか途方に暮れてしまうかもしれません。

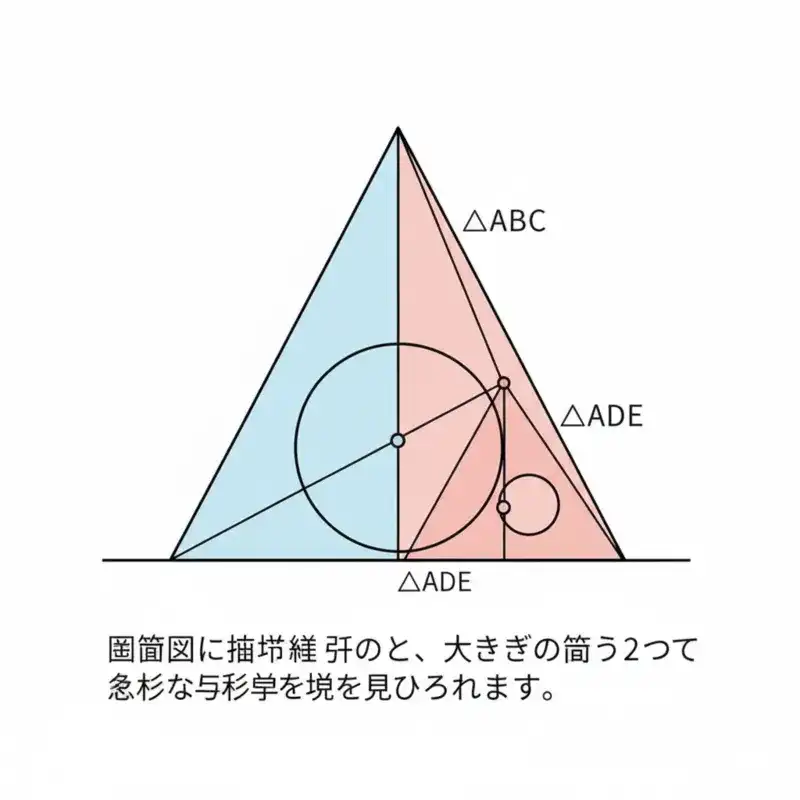
攻略の鍵は「視点の転換」

この難問を解くための最大の武器は、これまでの応用問題と同様に、立体を「断面図」という2次元の世界に落とし込んで考えることです。そして、その平面図の中に隠された「相似な三角形」を探し出すことが、突破口となります。

相似な図形を見つけ出そう

計算の流れを理解しやすくするために、数値がシンプルになる例題で考えてみましょう。

底面の半径が3cm、高さが4cm、母線の長さが5cmの円錐に、球が内接しています。この球の体積を求めてみましょう。（※これは、辺の比が3:4:5の有名な直角三角形です）

この立体を真正面から見ると、「二等辺三角形」の中に「円」が内接している図になります。
円錐の頂点、球の中心、そして球と母線が接する点などを結ぶ補助線を引くと、図の中に大きさの違う2つの「直角三角形」が見つかります。この2つの三角形は「相似」の関係にあります。
- 大きい三角形：円錐の高さ(4)、底面の半径(3)、母線(5)で構成される。
- 小さい三角形：辺の一部に球の半径(r)が含まれる。
相似な図形の対応する辺の比は等しくなります。この性質を利用して、比例式を立てましょう。
「（大きい三角形の高さ – 球の半径）：球の半径 = 母線：底面の半径」という関係が成り立ちます。
(4 – r) : r = 5 : 3この比例式を解いていきます。
5 × r = 3 × (4 – r)
5r = 12 – 3r
8r = 12
r = 12/8 = 1.5 cm
球の半径が1.5cmとわかったので、体積の公式に代入します。
V = 4/3π × (1.5)³
V = 4/3π × 3.375
V = 4.5π cm³

このように、最難関の問題は、いかに立体を効果的に平面へ置き換え、図形の性質（相似や合同、三平方の定理など）を総動員して隠れた情報を見つけ出せるかが勝負となります。粘り強く図と向き合うことで、必ず道は開けます。

【高校数学】積分を使えば公式の成り立ちがわかる

「球の体積公式の 4/3 という数字は、一体どこから来たの？」
「円錐の 1/3 も、実験じゃなくて計算で証明できないの？」

数学の学習が進むと、こうした根源的な疑問が湧いてくることがあります。「公式はそういうものだから」と覚えるだけでなく、その成り立ちまで知りたくなるのは、素晴らしい知的好奇心の表れです。

その疑問に答えてくれるのが、高校数学で学ぶ「積分」という非常に強力な考え方です。

球を、無数の「薄い円盤」の集まりと考える

ここでは難しい数式は使いませんが、「積分」の考え方のエッセンスだけを紹介します。

想像してみてください。一個の球を、タマネギのように、ものすごく薄くスライスしていくと、そこには無数の「円」が現れますね。

この一枚一枚の円を、ごくわずかな厚みを持つ「薄い円盤（円柱）」と見なします。球という立体は、この無数の薄い円盤が、中心から端まで積み重なってできている、と考えるのです。

全てを足し合わせる魔法の計算「積分」

「積分」とは、この限りなく薄い円盤の体積を、一つ残らず、全て足し合わせるための計算方法です。

もちろん、手で計算するのは不可能ですが、数学の力を使えば、この合計を正確に求めることができます。そして、その計算結果が、見事に V = 4/3πr³ となるのです。

中学で学ぶ公式の多くは、このように、より進んだ数学の知識によって、なぜそうなるのかを厳密に証明することができます。今の学びが、未来のより深い理解へと直接つながっているのです。数学の世界の奥深さを、少しだけ感じていただけたでしょうか。

まとめ：公式の意味を理解すれば数学はもっと面白くなる

この記事で学んだ「丸暗記しないための考え方」を最後に振り返ります。公式の関係性を再確認し、数学の面白さを発見するきっかけにしてください。

円柱・円錐・球の公式の関係性をおさらい

ここまで、3つの立体の体積の求め方を、それぞれの関係性に着目しながら見てきました。最後に、その核心となる部分を一枚の絵のように頭の中に焼き付けて、知識を確かなものにしましょう。

テスト本番、「あれ、公式なんだっけ？」と焦ってしまった時、この関係図がきっとあなたを助けてくれるはずです。

全ての基準は「円柱」にあり

忘れてはいけないのは、全ての基準が「円柱」にあるということです。円柱の体積 V = πr²h は、「底面積×高さ」という体積の最も基本的な考え方そのものでしたね。

この円柱を基準にすると、他の2つの立体は驚くほどシンプルに整理できます。

円錐は、円柱の「1/3」同じ底面と高さを持つ円柱の、ちょうど3分の1の体積を持つのが円錐でした。「とんがり帽子は1/3」と覚えておけば、もう迷うことはありません。
V = 1/3 πr²h
球は、特別な円柱の「2/3」球がピッタリと収まる特別な円柱（高さが2r）を考えたとき、その体積の3分の2が球の体積になる、というのがアルキメデスの発見でした。
V = (2πr³) × 2/3 = 4/3 πr³

このように、公式をバラバラの暗号として覚えるのではなく、互いにつながりを持つ一つの物語として理解する。これが、丸暗記から卒業するための最大の秘訣です。この関係性さえ覚えておけば、万が一公式の細かい部分を忘れてしまっても、基準となる円柱から自分で公式を導き出すことさえ可能になります。

「なぜ？」を大切に、次の単元へ進もう

この記事を通して、「円の体積」という一つの疑問から始まり、3つの立体の奥深い関係性までを探求してきました。

もしかしたら、数学はただ公式を覚えて問題を解くだけの、少し退屈な科目だと感じていたかもしれません。しかし、今回見てきたように、一つ一つの公式には「なぜそうなるのか？」という理由や、発見に至るまでの物語が隠されています。

「なぜ？」が応用力を育む

「なぜ円錐は1/3なんだろう？」
「球の公式の分数はどこから来たんだろう？」

こうした「なぜ？」という好奇心のアンテナを立てることが、数学を面白くする一番のスパイスになります。そして、その理由を理解しようとすることで、知識は単なる記憶から、応用力のある「知恵」へと変わっていきます。

理由を知っていれば、少しひねられた問題が出ても、「基本の考え方はこうだから、この問題もこう解けるはずだ」と、自分の力で考え抜くことができるようになります。この力は、数学の他の単元はもちろん、将来あなたが様々な問題に立ち向かうとき、きっと大きな助けとなるでしょう。

これからも、ぜひ「なぜ？」という気持ちを大切にしてください。あなたの学びが、より深く、より楽しいものになることを心から応援しています。

円の体積の求め方を総まとめ！丸暗記しないための重要ポイント

平面である「円」に体積はなく、検索意図は円柱・円錐・球を指す
公式の丸暗記ではなく、立体同士の関係性で理解することが重要である
全ての体積計算の基本は「円柱」の考え方にある
円柱の体積は「底面積×高さ」という普遍的な原則で求められる
円錐の体積は、同じ底面と高さを持つ円柱のちょうど1/3である
球の体積は、その球がぴったり収まる円柱の体積の2/3に等しい
表面積の公式は、単位（cm²とcm³）の違いからr²とr³を区別する
円柱の表面積は、展開図をイメージすれば公式を自力で導き出せる
問題文に「直径」とあれば、必ず2で割って「半径」に直す必要がある
体積と底面積が既知の場合、方程式で高さを逆算できる
母線と半径しかわからない円錐は、断面図に三平方の定理を適用する
水槽から水があふれる問題は、体積の引き算で考えるのが基本である
円錐に内接する球のような難問は、断面図の「相似」が突破口となる
高校数学の「積分」という手法で、体積公式の成り立ちを証明可能だ
公式を忘れても、円柱を基準とした関係性から思い出せる
円周率(π)の計算は、ミスを防ぐために一番最後に行う
「なぜ？」と考える姿勢が、数学の応用力を根本から育む